Loss Function - Cross Entropy

#ml/basic

Talk about entropy first

A good video explain what is entropy well ^[1]

An example from weather station

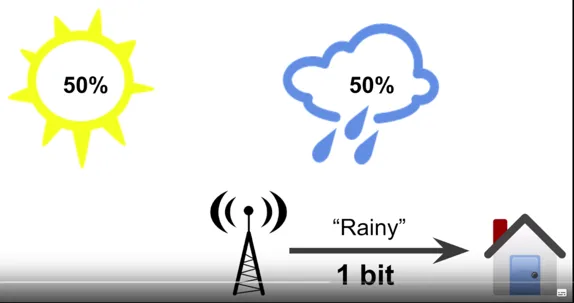
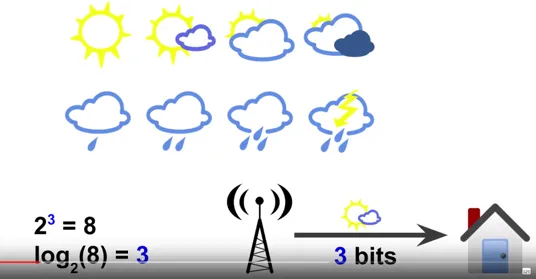
A weather station reports a 50/50 change of rain or sunshine, we can use 1 bit to represent the weather information. If we have more weather status, we can use more bit to represent it, for example there are 8 weather status, we can use 3 bits to represent it.

Here's the formula:

50/50 sunny or raining: $l o g_{2} (2) = 1$ , so use 1 bits
8 weather status: $l o g_{2} (8) = 3$ , so use 3 bits

Then what is the probability is not equal ... ?

event	probability	entropy
sunny	0.75	$- l o g_{2} (0.75) = 0.415$
raining	0.25	$- l o g_{2} (0.25) = 2$
total: $0.75 \times 0.415 + 0.25 \times 2 = 0.811$

As a result, we can calculate the entropy by the following formula:

H (p, q) = - \sum_{x} p (x) \log q (x)

where

$p (x)$ : the true probability distribution
$q (x)$ : the predicted probability distribution

entropy log 2 or log e ?

it doesn't matter log base 2 or base e, in most cast if you are calculating the digital information or communication, base 2 is preferred, but for other question, we can use another log base.

Now it's cross entropy turn

Cross entropy measures the difference between two probability distributions.

Now, we take a machine learning problem, we need to use a loss function to evaluate how close the predicted value and actual value, so that we can compensate the error back to the model, to enhance the accuracy.^[2]